1. はじめに(検証の目的)
PixInsight に最近追加された新しいストレッチツール
MAS(Multiscale Adaptive Stretch)
第一印象としては、
- 自然
- 破綻しにくい
- 淡い構造が出やすい
と感じる一方で、
「これ、普段使っている PixelMathUI と何が違うの?」
「STF→HT と比べて何が優れているの?」
という疑問も正直ありました。
そこで今回は、
“見た目”ではなく “数値” で違いを確認する ことを目的に、
- PixelMathUI
- MAS
- STF → HistogramTransformation(HT)
の 3手法 を局所コントラスト(Local Contrast) という指標で比較・検証してみました。
※その他のストレッチツールは定量評価が難しいと判断したため今回は除外しました。
2. MAS(Multiscale Adaptive Stretch)とは?
MAS の基本的な考え方
MAS(Multiscale Adaptive Stretch)は名前の通り、
- Multiscale(多段階スケール)
- Adaptive(局所適応型)
- Stretch(非線形ストレッチ)
を組み合わせたストレッチ手法です。
従来の STF → HT が
「ヒストグラム全体を一括で変形」するのに対し、
MAS は
画像を複数の空間スケールに分解し、
各スケールごとに最適なストレッチ量を自動適応させる
という発想に基づいています。
機能としては以下のとおり
・ストレッチ後の希望する背景レベルを指定
・クリッピングポイントを設定
・アダプティブストレッチ中に高輝度領域のコントラストを制御
・マルチスケールコントラスト回復エンジン
・大規模画像コンポーネントと小規模画像コンポーネントを分離するために、マルチスケール中央値変換(MMT)で使用されるダイアディックスケールの数の設定
・HSV色空間の彩度チャンネルに曲線変換を適用し、色の鮮やかさを高めながら、背景をクロミナンスノイズ増幅から保護
・色彩度が有効になっているときの彩度強化の強度を制御
・彩度範囲全体の彩度強化の分布を制御
使用方法についは、
The MultiscaleAdaptiveStretch Tool または、PixInsightアプリ内のドキュメントを参照してください。
PixelMathUI との思想的な違い
| 項目 | PixelMathUI | MAS |
|---|---|---|
| 操作 | ユーザーが明示的に式で制御 | アルゴリズム主導 |
| 強調傾向 | コントラストが立ちやすい | 穏やかで破綻しにくい |
| 再現性 | 設定依存 | 比較的安定 |
| 星への影響 | 強く出やすい | 抑制されやすい |
PixelMathUI は
「意図した表現を作り込む道具」
MAS は
「破綻しない方向へ自動で寄せてくれる道具」
という性格の違いがあると感じます。
3. 今回の検証方法
使用データ

- 対象:NGC1499(カリフォルニア星雲)
- 使用画像:WBPP→Crop→BlurXTerminator(CorrectOnly)→SFC→MGC→SPCC L画像
- 比較方法(以下のツールで上記のL画像をストレッチして比較、各値は画像のとおり)
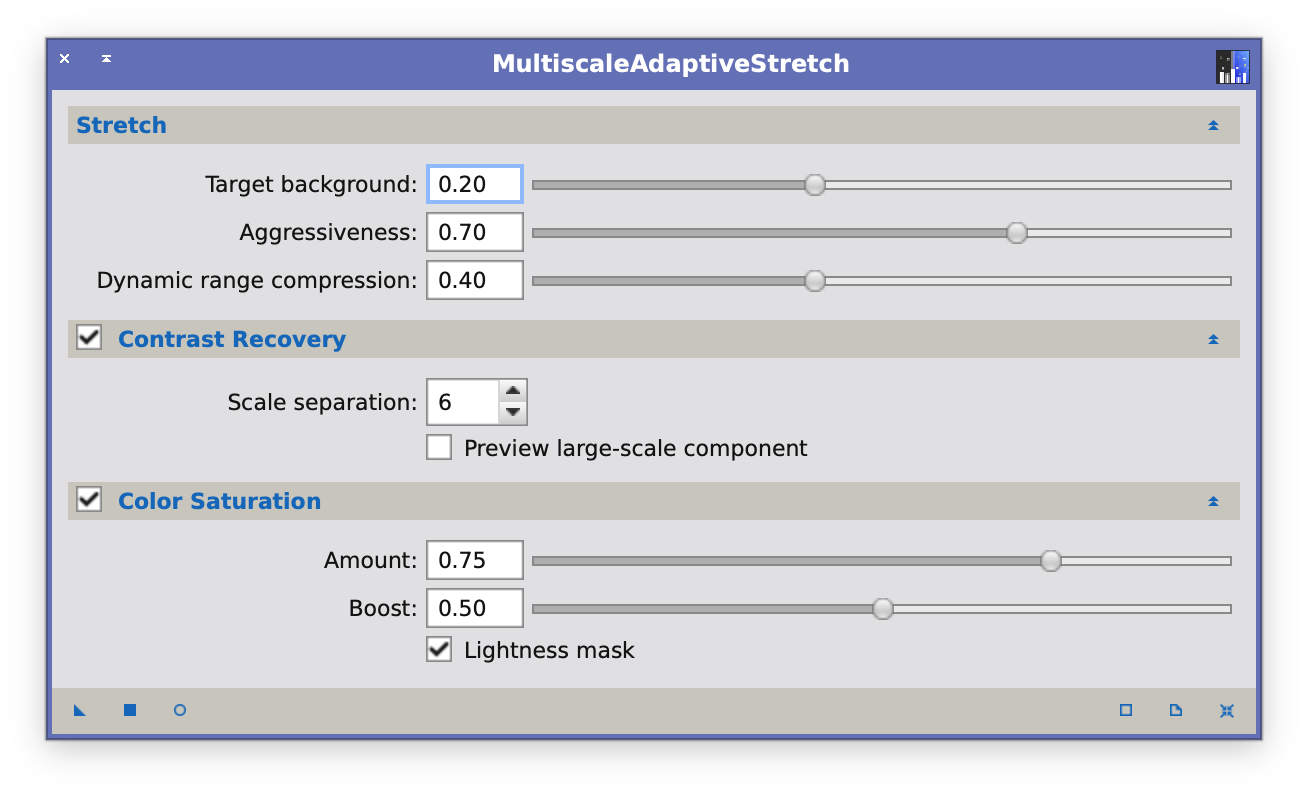
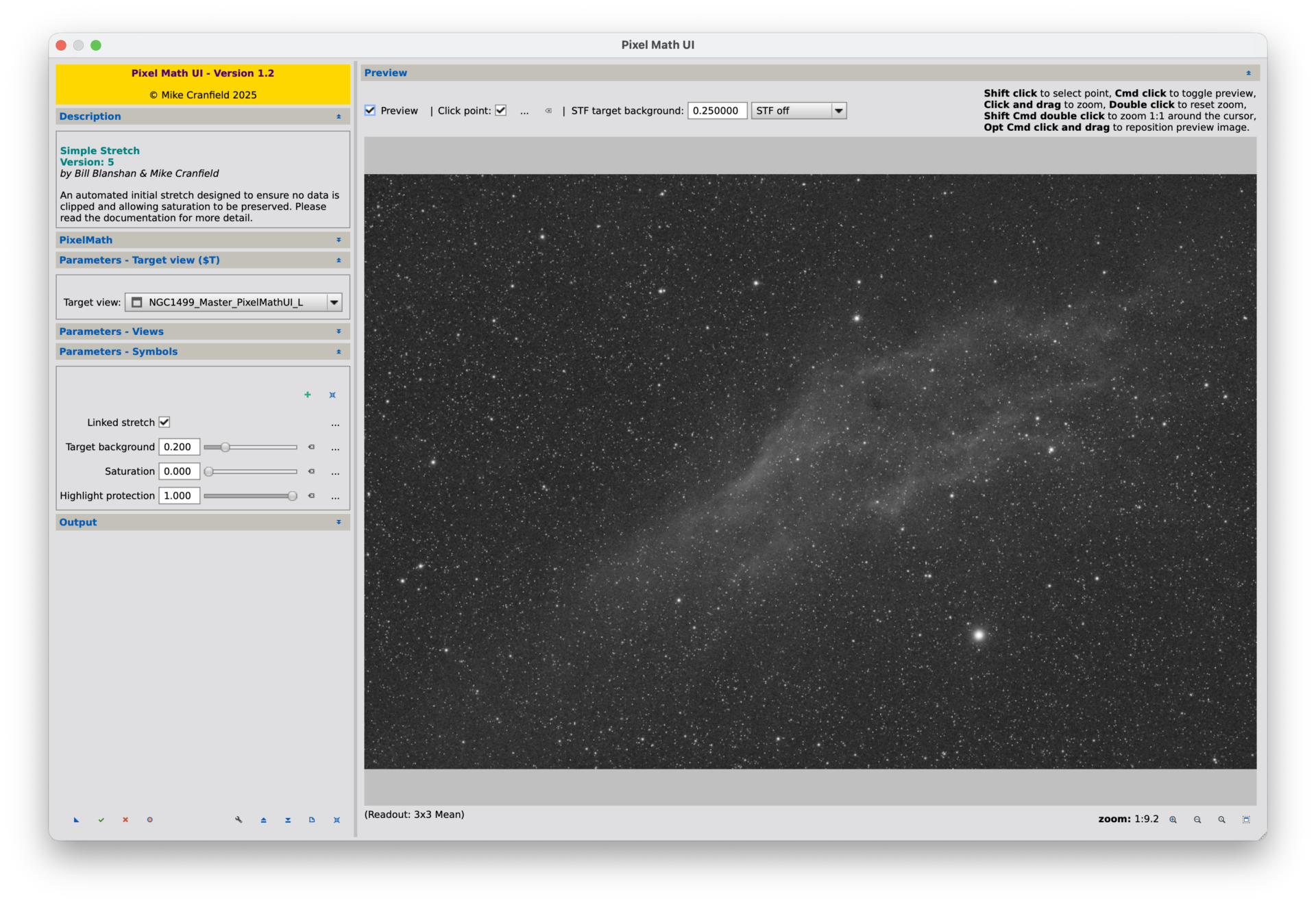
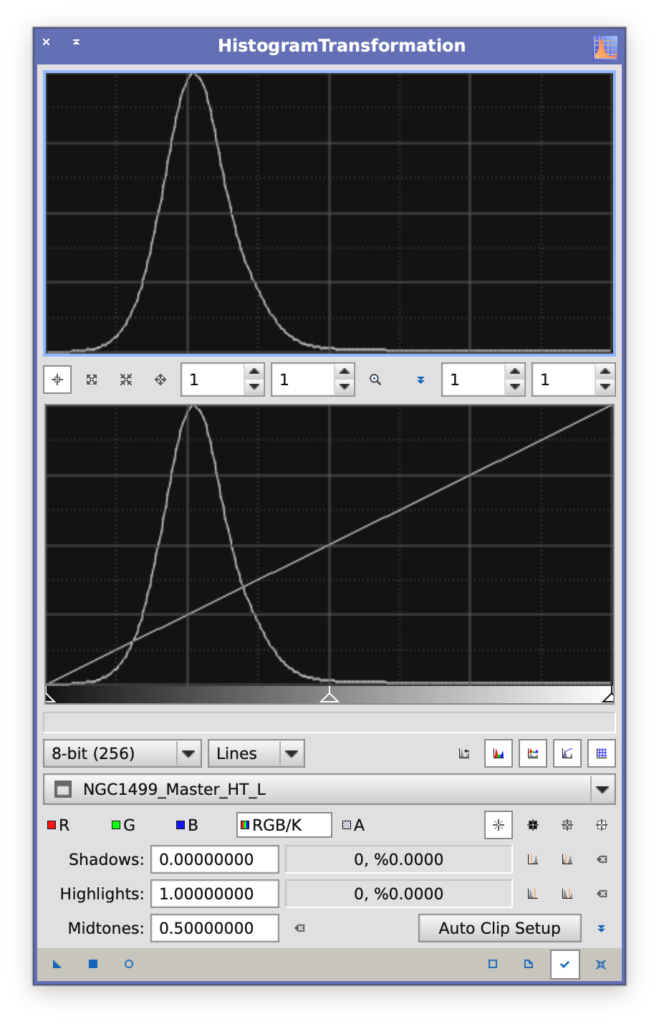
コントラストの定義
今回使用した指標は以下です。Local Contrast=μlocalσlocal
- μ:局所平均
- σ:局所標準偏差
- window:評価窓サイズ(px)
PixInsight の LHE や MMT とも親和性の高い、
「構造の立ち具合」を数値化した指標です。
評価スケール(window)
| window | 意味 |
|---|---|
| 32px | 微細構造・星の影響が強い |
| 64px | 中間スケール(星雲構造) |
| 128px | 大域構造・滑らかさ |
そもそも「コントラスト」とは何を測りたいのか
天体画像で言うコントラストは、単に
- 明るい / 暗い
ではなく、
周囲と比べて、どれだけ変化があるか
です。
PixInsight的に言えば:
- 星雲の筋がどれだけ浮き上がるか
- 星がどれだけ目立つか
- 背景がどれだけザラつくか
これらを 定量化したい、というのが目的です。
今回使っているコントラストの定義
このプログラムで使っている指標は:Local Contrast=μlocalσlocal
です。
| 記号 | 意味 |
|---|---|
| μ (mu) | 局所平均輝度 |
| σ (sigma) | 局所標準偏差 |
| σ / μ | 相対的な局所コントラスト |
なぜ「局所平均」と「局所標準偏差」なのか
🔹 局所平均 μ(local mean)
- その場所の「明るさの基準」
- 背景なのか、星雲なのか、星なのか
PixInsightで言えば:
- BackgroundModel
- Local normalization
- LHE の「基準輝度」
に近い概念です。
🔹 局所標準偏差 σ(local std)
- その範囲での「揺らぎの大きさ」
- 変化が大きい → σが大きい
例:
- 星がある → σ 大
- フィラメント → 中
- 滑らかな背景 → 小
👉 構造・星・ノイズを全部含んだ“変動量”
なぜ σ だけではダメなのか?
問題点
σだけを見ると:
- 明るい場所ほど σ が大きくなりがち
- 暗部は不利
つまり、
「明るいからコントラストがある」
と誤判定してしまう
なぜ μ で割るのか(超重要)
にすると:
- 明るい場所 → 正規化される
- 暗い場所 → 相対的な変化が見える
直感的に言うと
| 状況 | σ | μ | σ/μ |
|---|---|---|---|
| 明るいが均一 | 小 | 大 | 小 |
| 暗いが構造あり | 中 | 小 | 中 |
| 星 | 大 | 中 | 大 |
👉「その明るさに対して、どれだけ暴れているか」
を測っていることになります。
「局所(Local)」であることの意味
この計測は 全画像ではなく、窓(window)ごと に行っています。
window サイズの意味
| window | 見ているスケール |
|---|---|
| 32 px | 星・微細ノイズ |
| 64 px | フィラメント |
| 128 px | 大域背景 |
PixInsightで言えば:
- LHE の Radius
- MMT の layer scale
とほぼ同じ役割です。
実際にやっている処理(イメージ)
各ピクセルについて:
- 周囲 window×window を切り出す
- その中の
- 平均 μ
- 標準偏差 σ
を計算
- そのピクセルの「コントラスト値」を
σ/μ として記録
評価方法(Pythonプログラム概要)
- 画像を 0–1 正規化
- 指定 window サイズで局所平均との差分散を計算
- 以下を可視化・数値化
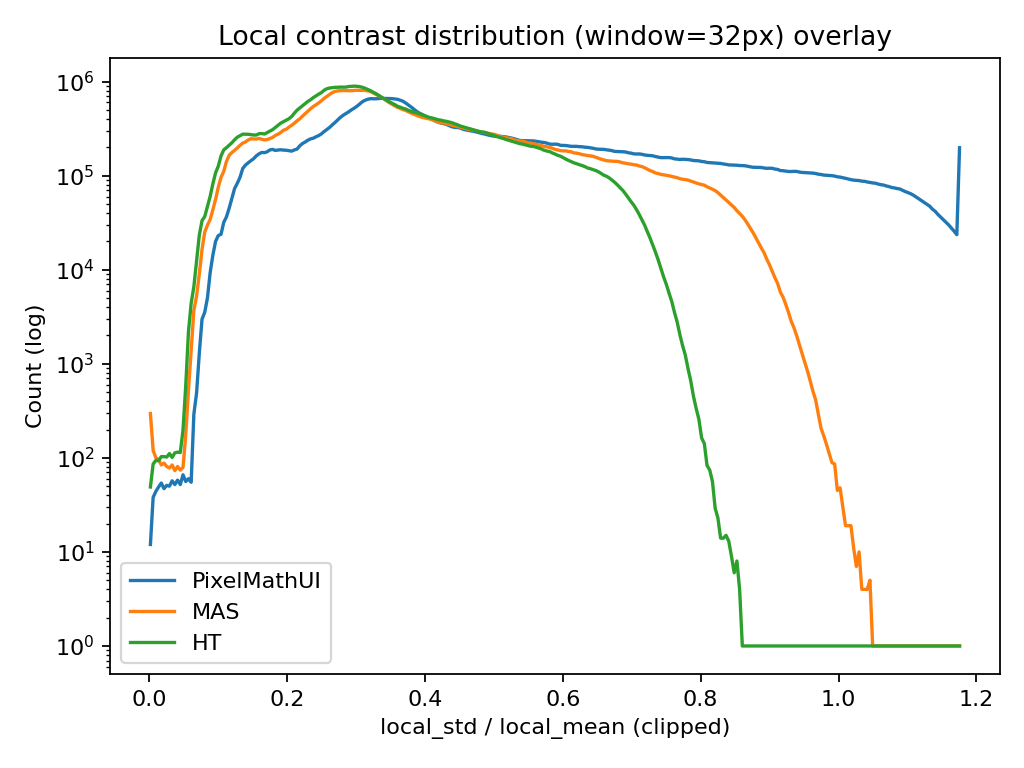
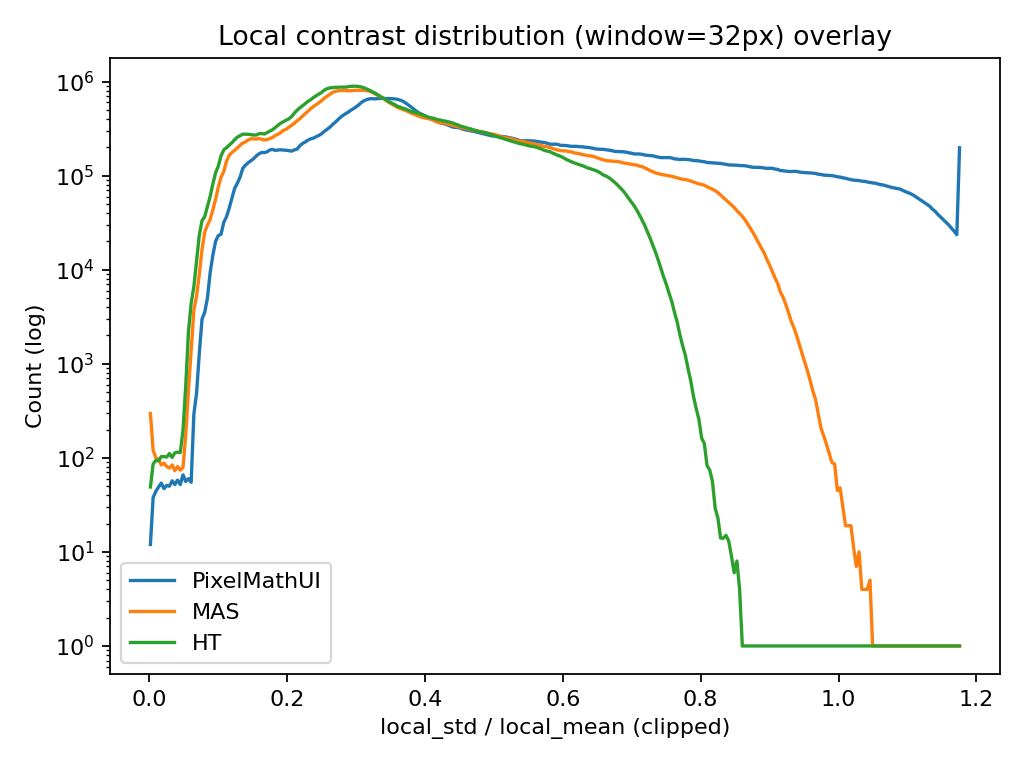
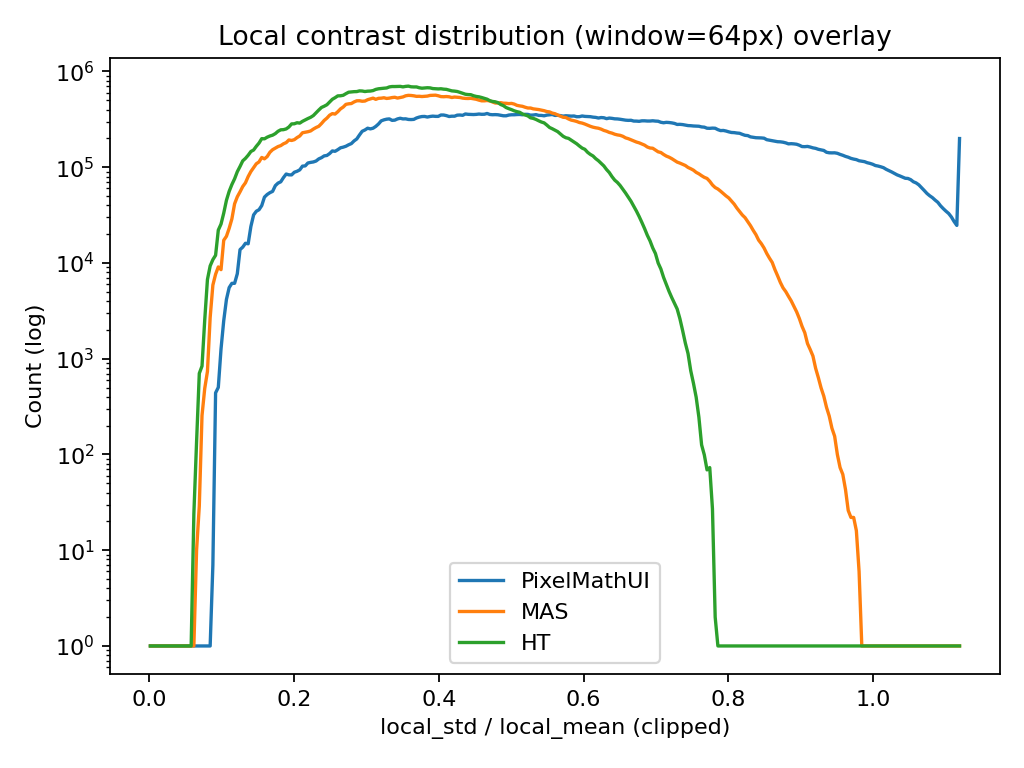
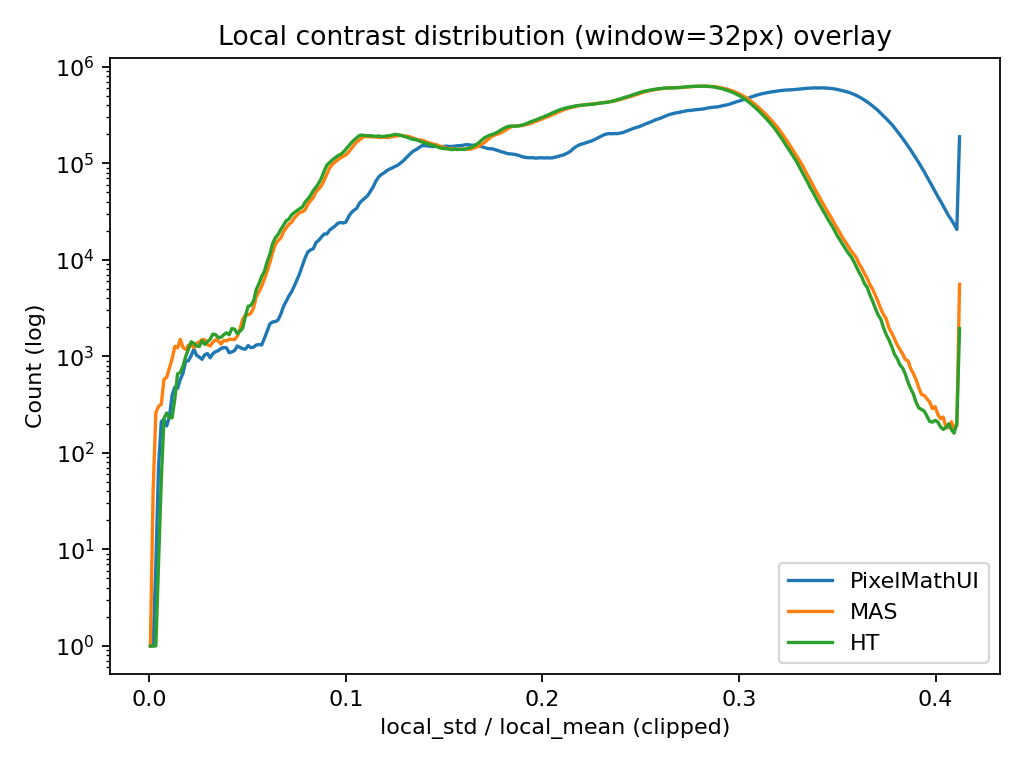
🔹 分布の重ね描き(ヒストグラム)
何を見ている?
- ローカルコントラスト値(local_std / local_mean) の分布
- 横軸:コントラストの強さ
- 縦軸:その強さを持つピクセル数(logスケール)
何が分かる?
- 右に伸びるほど「強いコントラストを持つ領域が多い」
- PixelMathUI / MAS / HT の
- どれがより攻めたコントラストを作っているか
- 裾(テール)がどこまで伸びているか
読み方(今回の検証的に)
- PixelMathUI
→ 右側に長い裾=局所的に非常に強いコントラスト - MAS
→ 分布は広いが、裾は抑制されている - HT
→ 全体に左寄り=穏やか
📌 「どれが一番派手か」ではなく
「どれがどのレンジを使っているか」を見る図
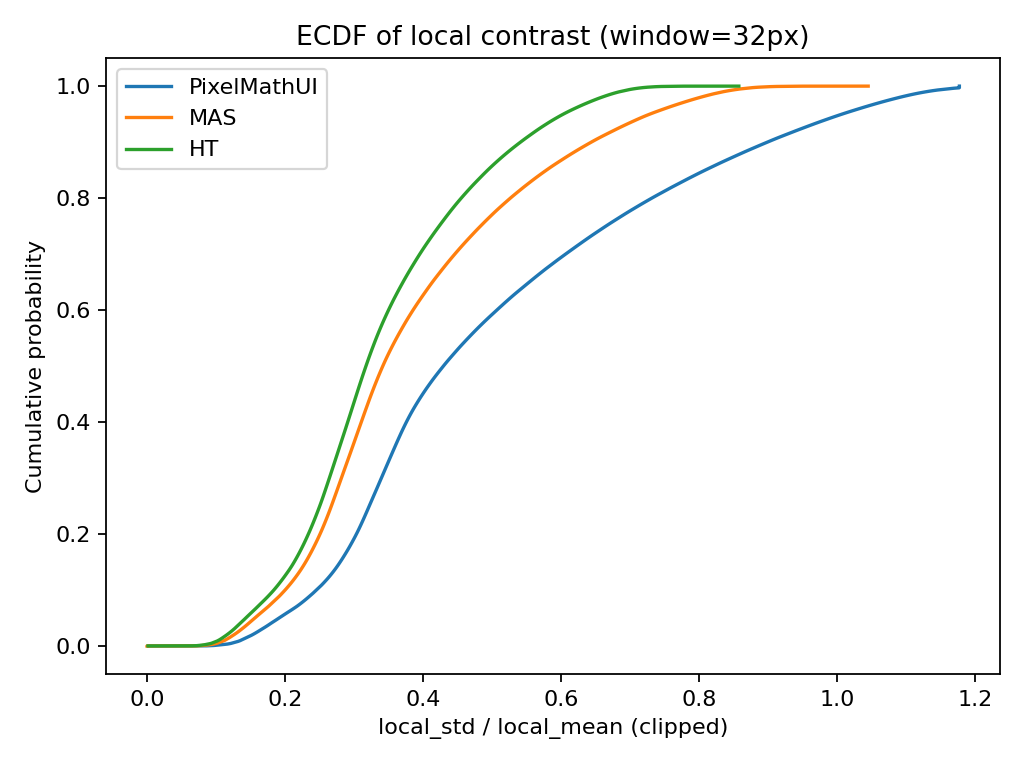
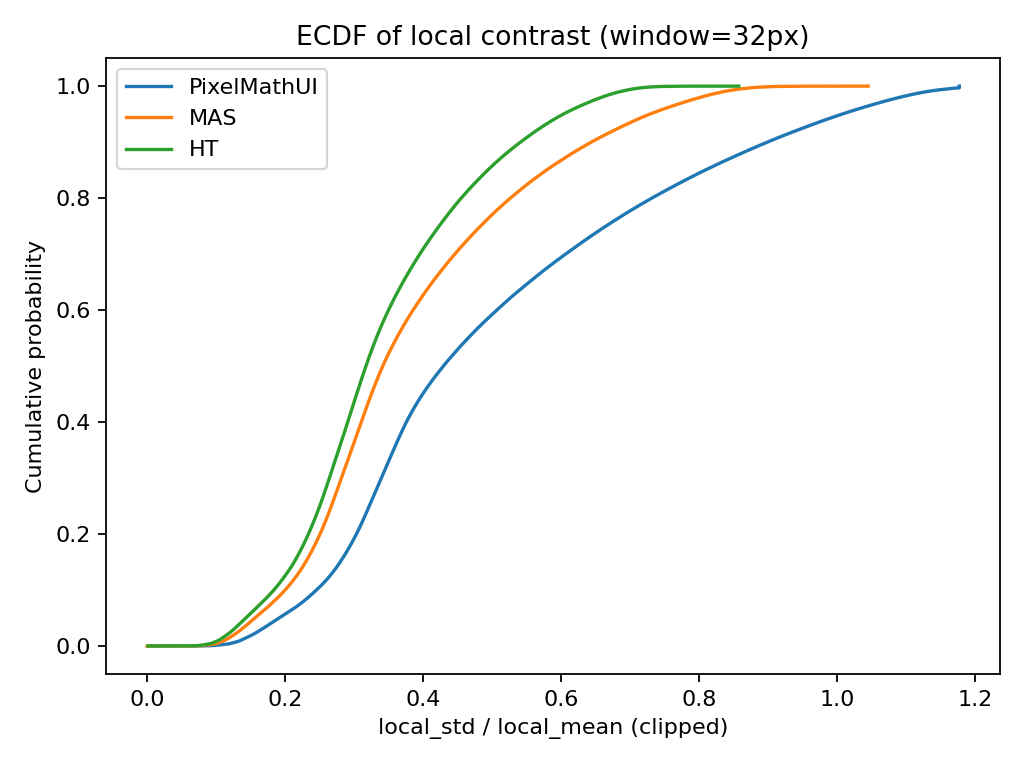
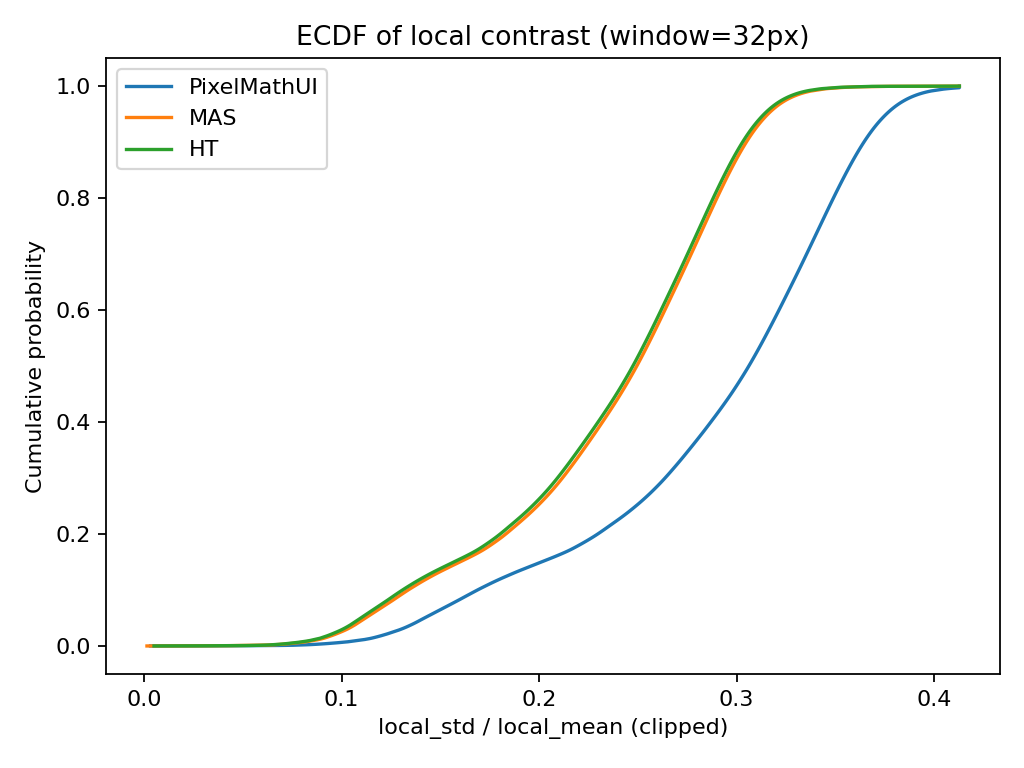
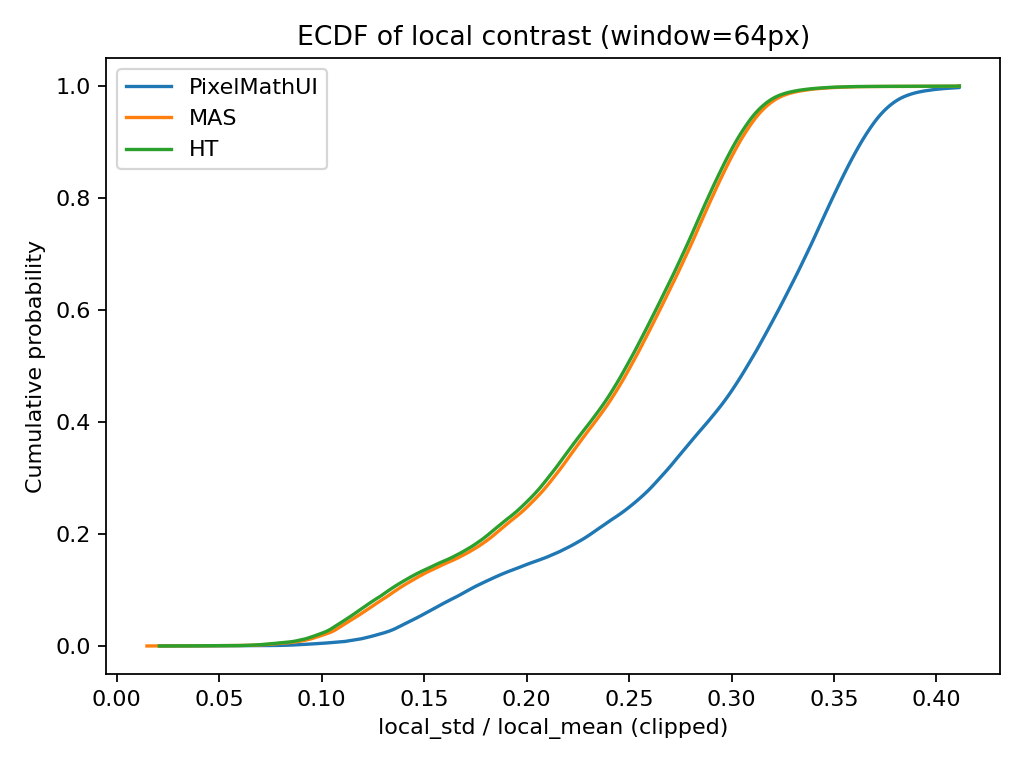
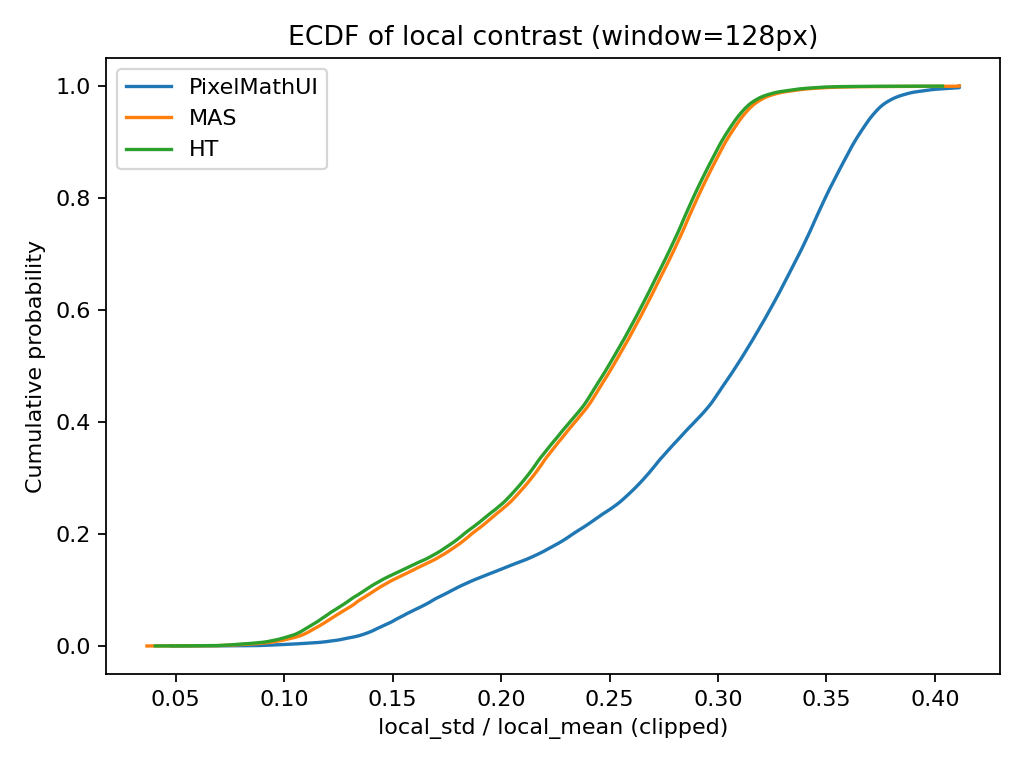
🔹 累積分布(ECDF)
何を見ている?
- 「このコントラスト以下の画素が 全体の何% か」
- 分布の差が一目で分かる
何が分かる?
- 曲線が 右に行くほど → 全体としてコントラストが強い
- 曲線が 急 → コントラストが均一
- 曲線が なだらか → コントラストに幅がある
読み方(重要)
- PixelMathUI
→ 上位◯%が非常に高コントラスト - MAS
→ 中位〜高位がなだらかに伸びる - HT
→ 早い段階で頭打ち
📌 「どのツールが “一部だけ強い” のか
それとも “全体を底上げしている” のか」が分かる
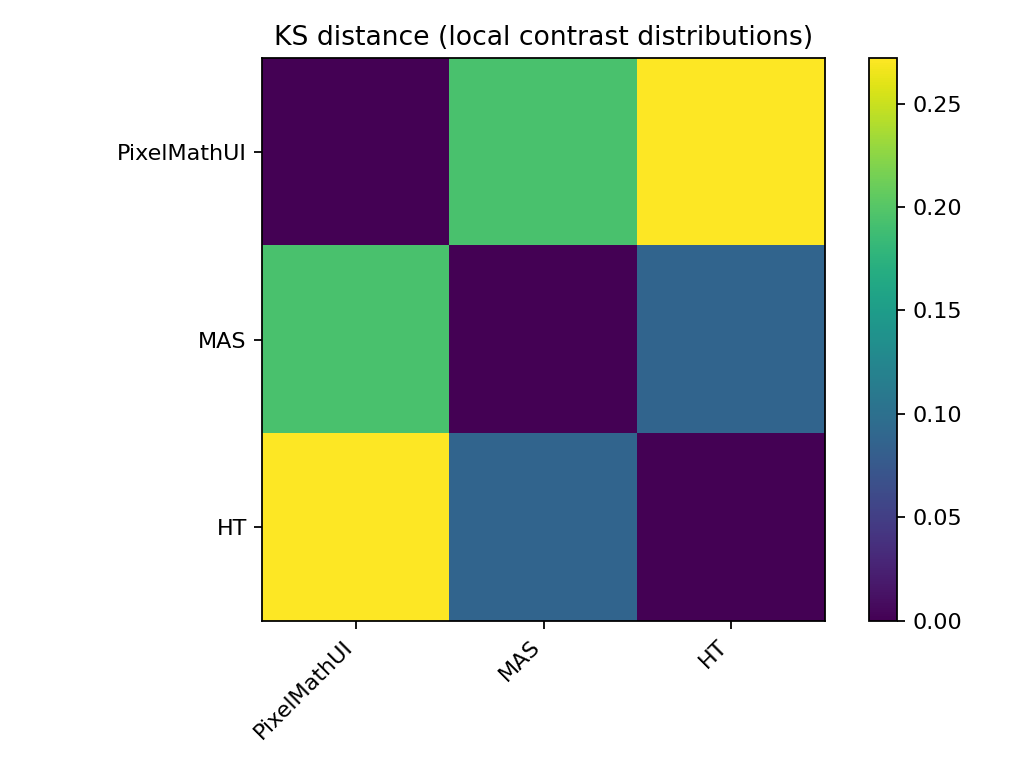
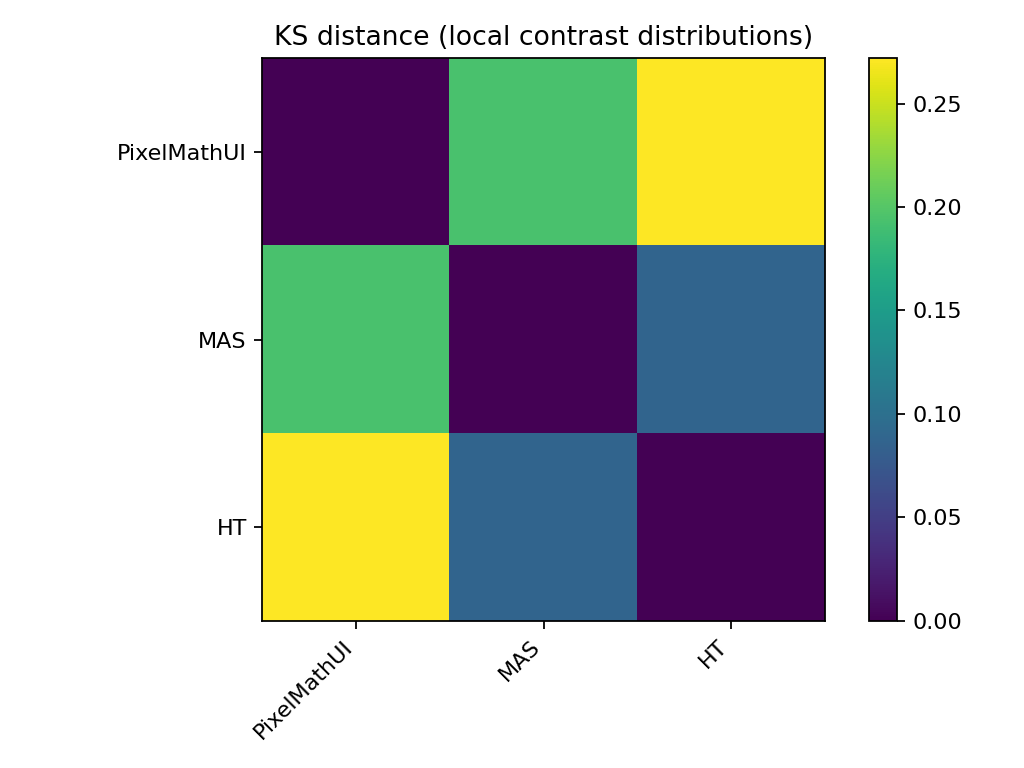
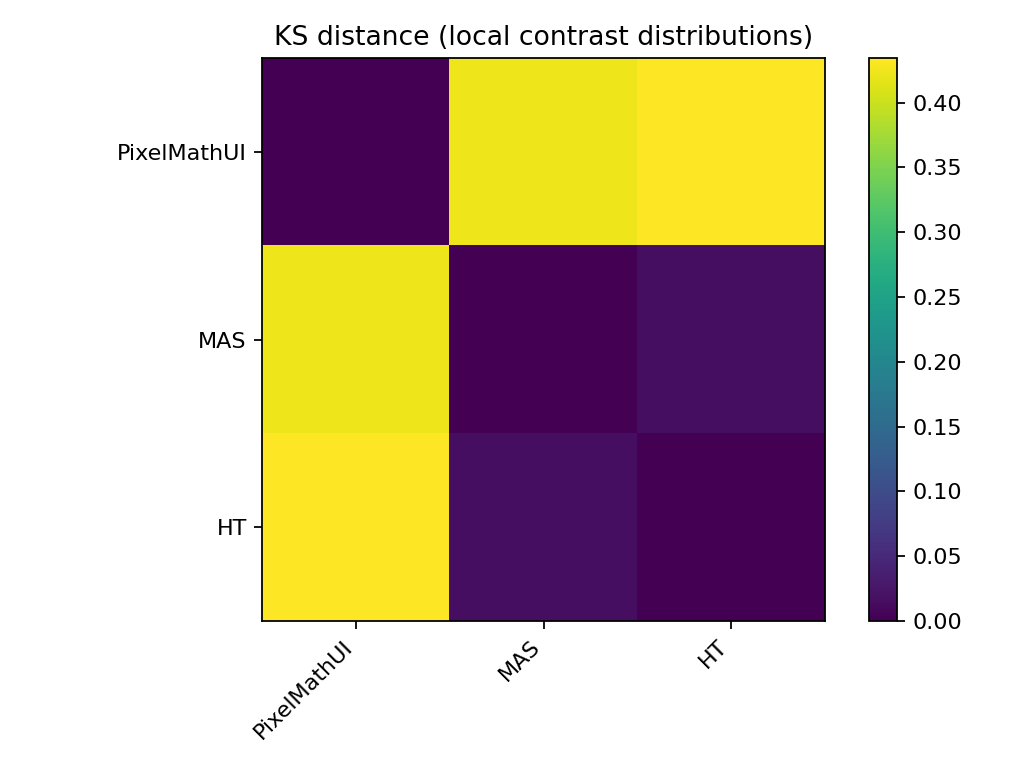
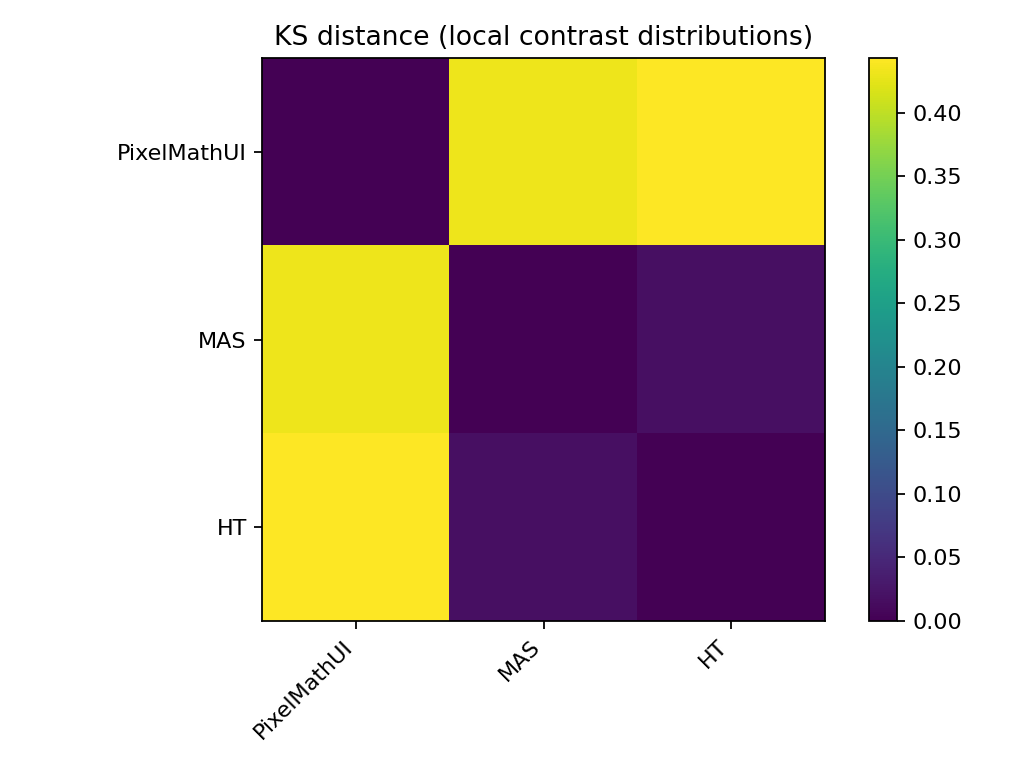
🔹 KS距離(分布差の強さ)
何を見ている?
- 2つの分布がどれだけ違うか
- 値が大きいほど「性格が違う」
読み方
- PixelMathUI ↔ MAS
→ 距離が大きい → 明確に別物 - MAS ↔ HT
→ 中間的距離 → 似ているが完全一致ではない
📌 「MASはHTの単なる改良版ではない」
ことを数値で裏付け

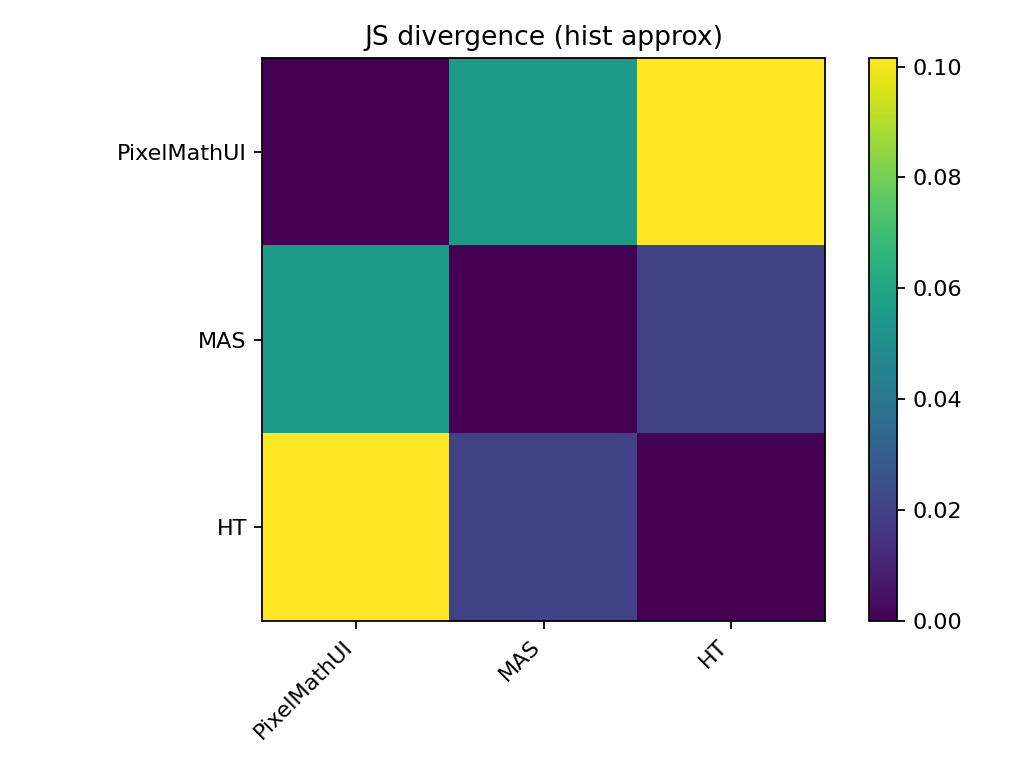
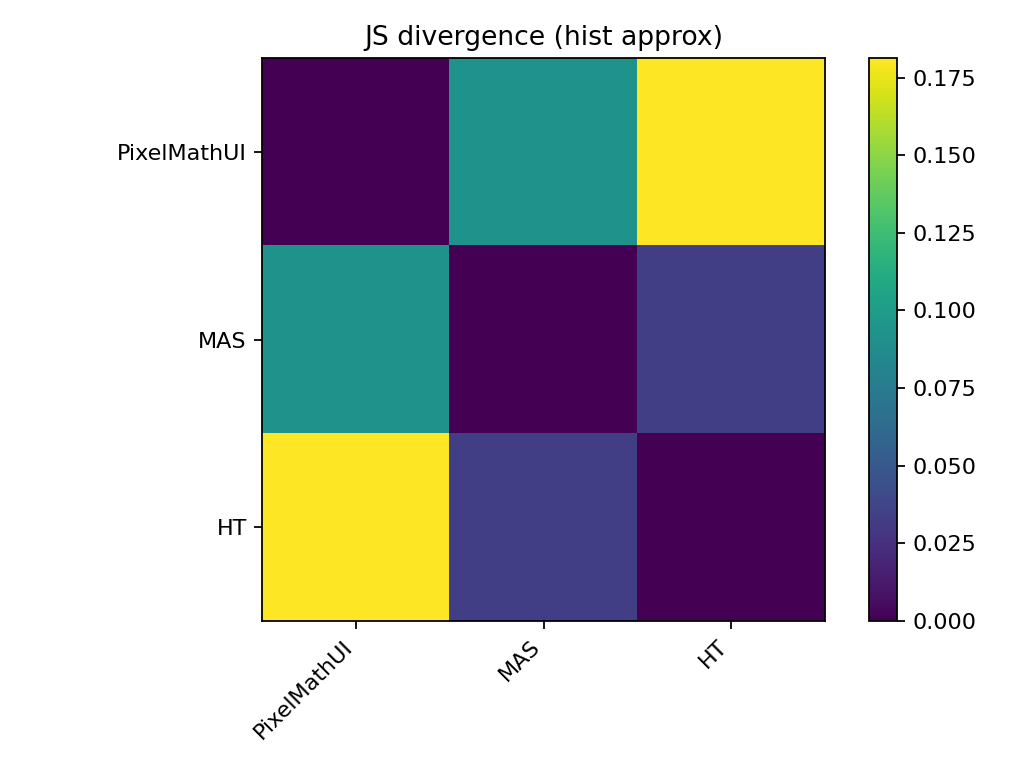
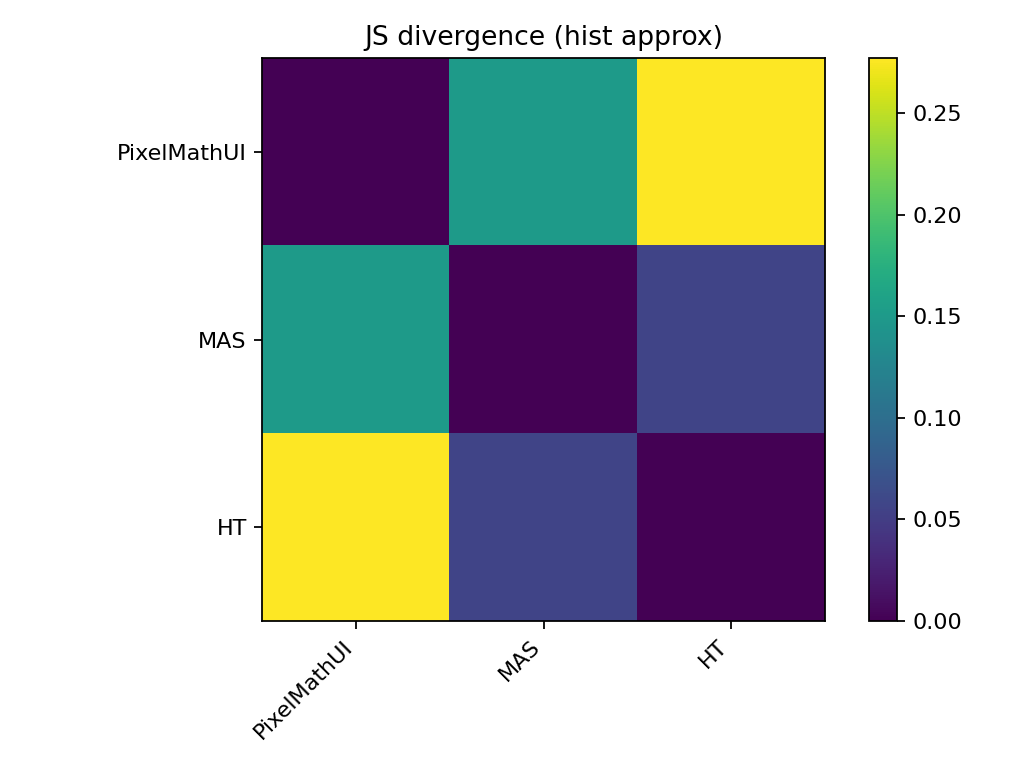
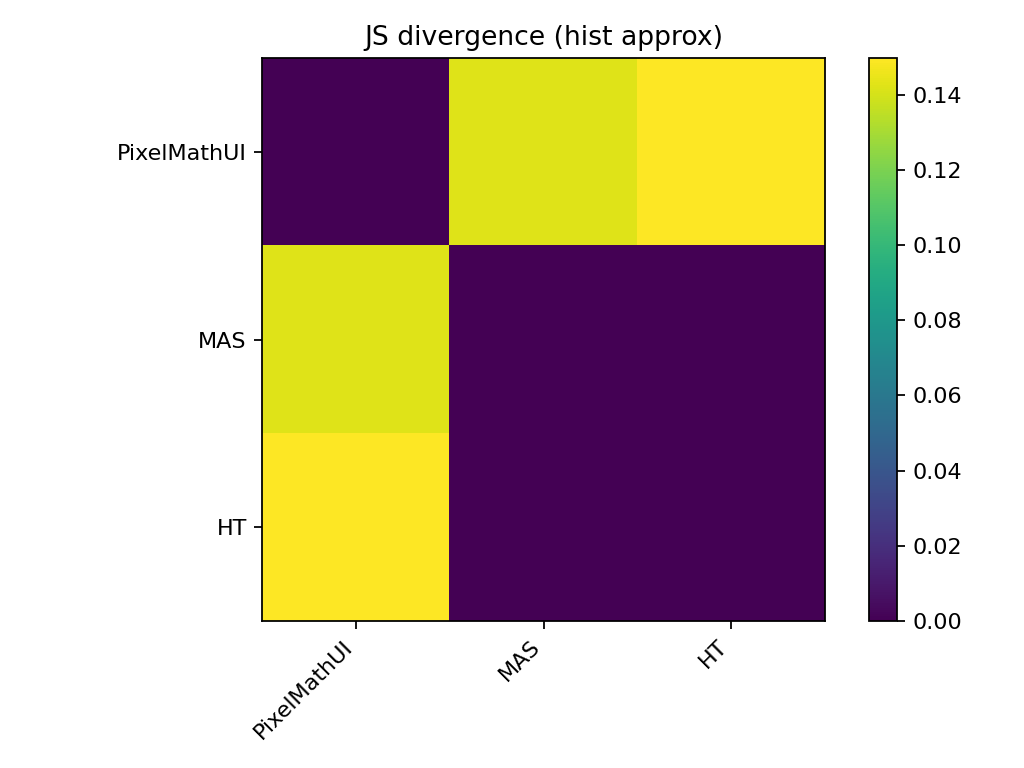
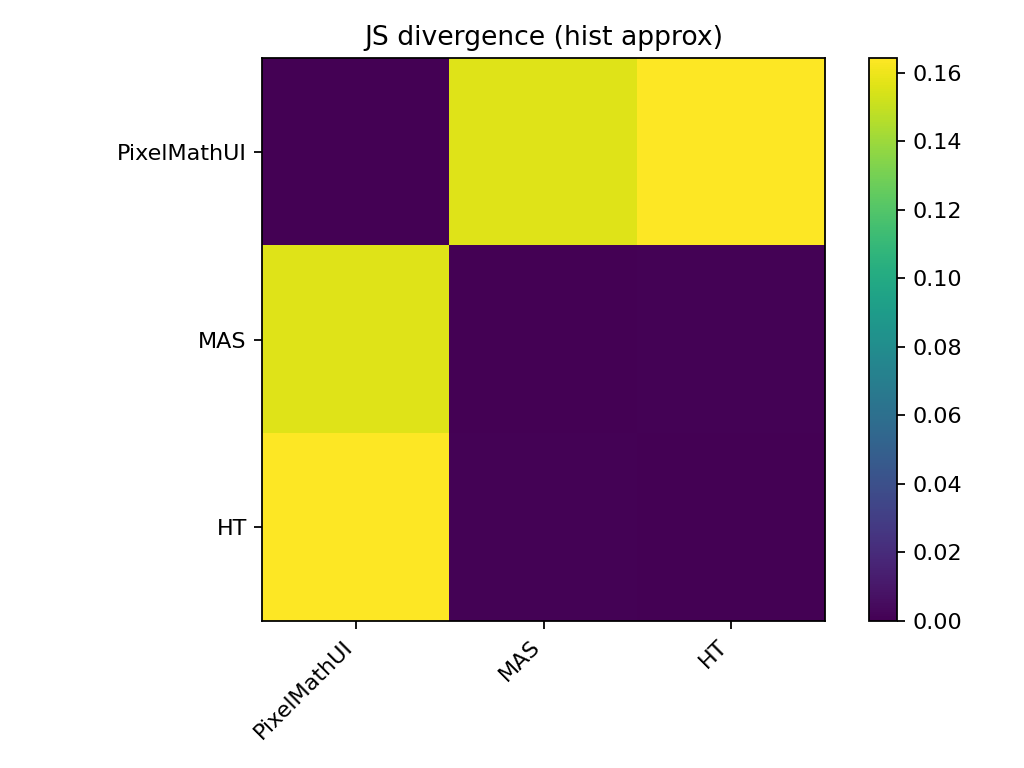
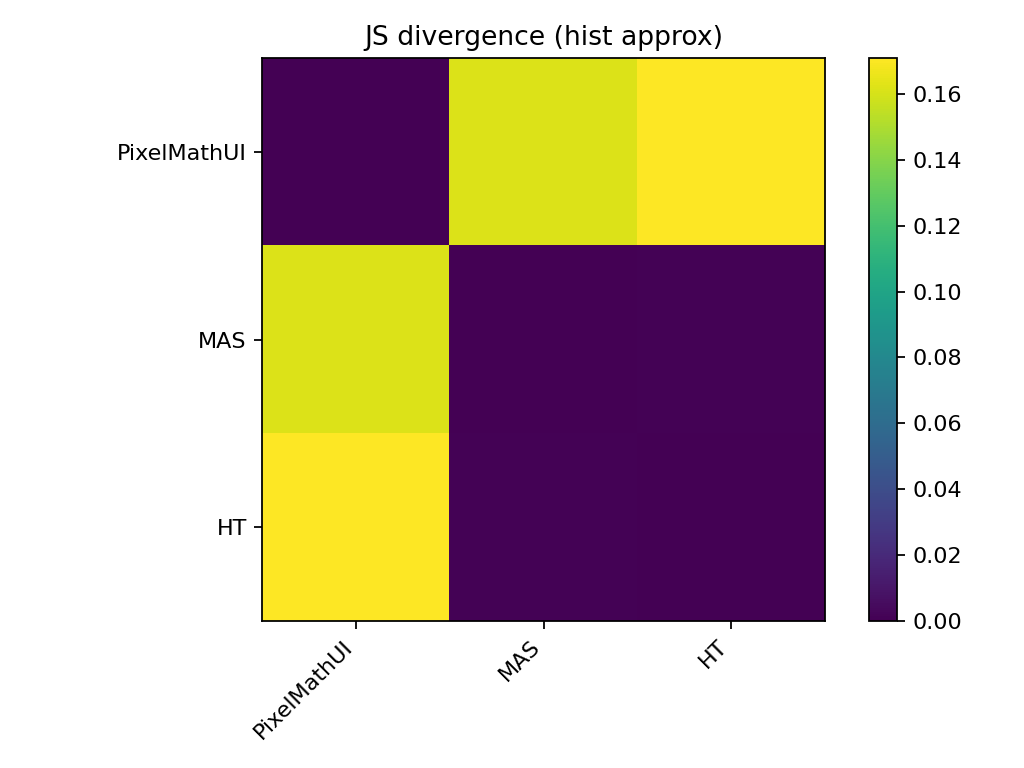
🔹 JSダイバージェンス(情報量の差)
KSとの違い
- KS:最大差
- JS:分布全体の形状差
読み方
- 値が大きいほど
→ コントラストの使い方が違う
📌 PixelMathUI は
「一部を強くするタイプ」
MAS は
「分配の仕方が違うタイプ」
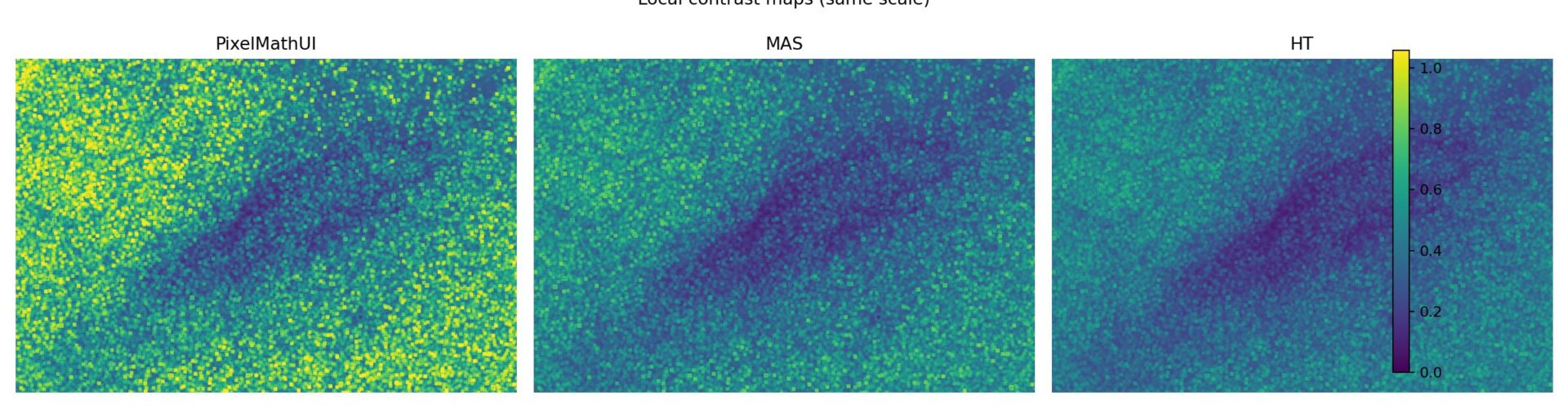
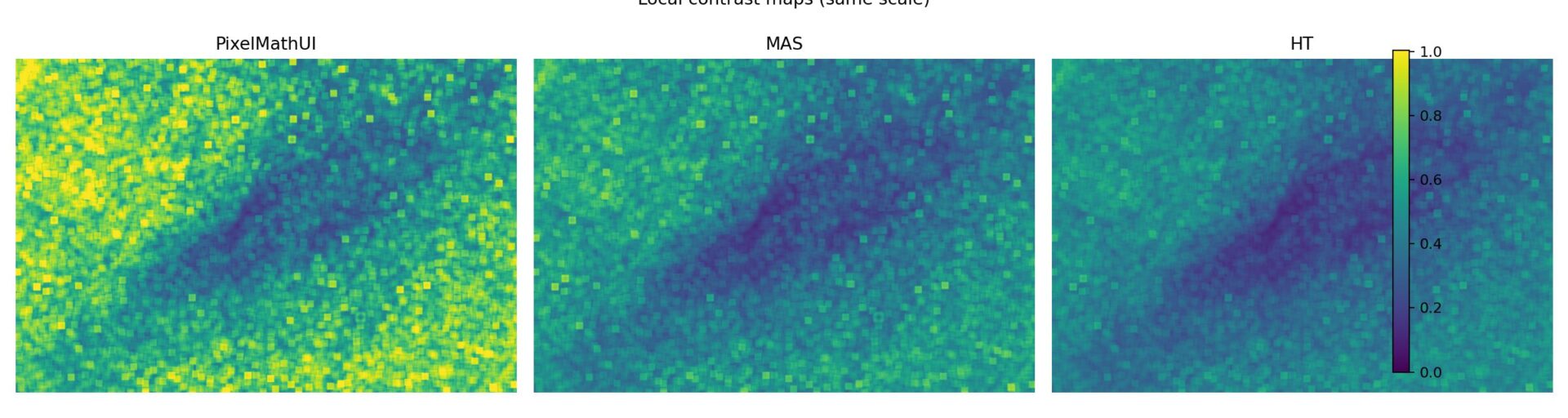
🔹 ローカルコントラストマップ並べ
何を見ている?
- 「どこでコントラストを作っているか」
- 同一スケールで比較
読み方
- 明るい部分=コントラストが高い
- 星周り / フィラメント / 境界
観察ポイント
- PixelMathUI
→ 星周り・エッジが強く光る - MAS
→ 構造内部まで滑らかに反応 - HT
→ 全体に均一
📌 “数値がどこに現れているか”を可視化

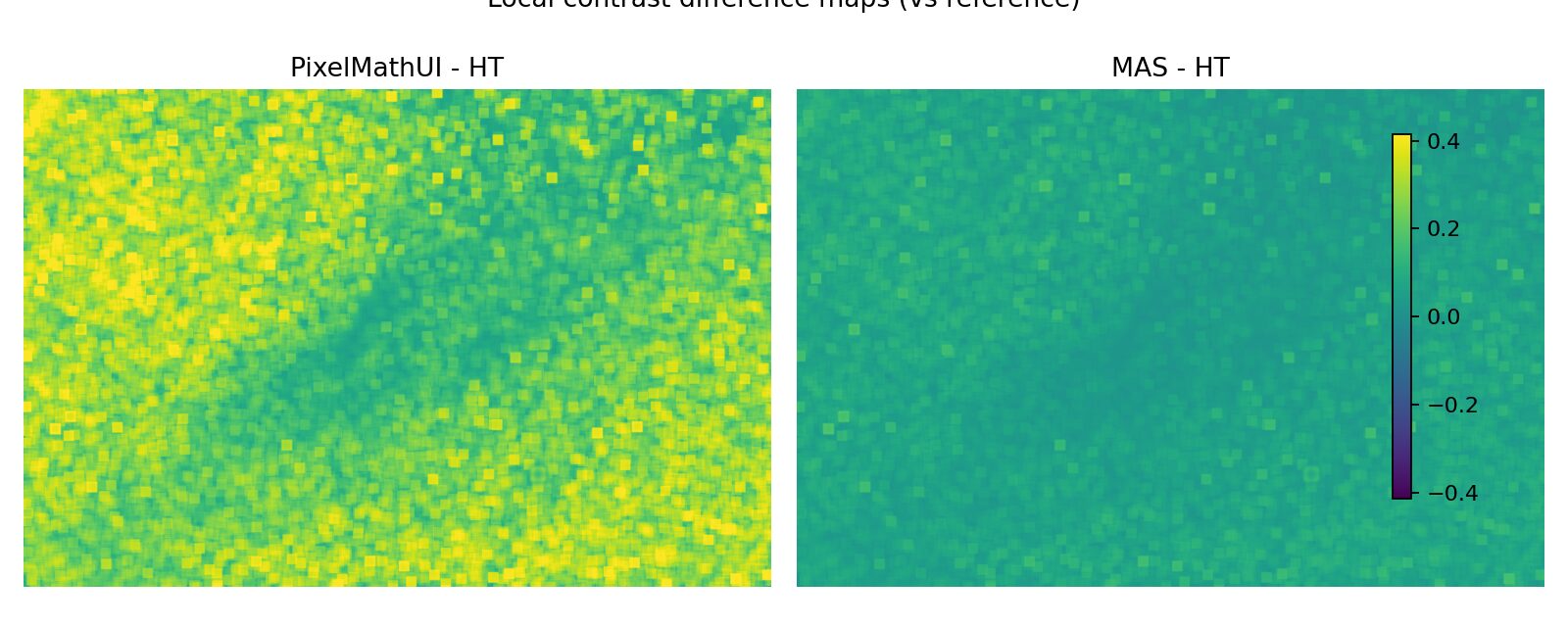
🔹 基準との差分マップ
何を見ている?
- 「どこが 増えた / 減った か」
読み方
- 明るい:基準より強い
- 暗い:基準より弱い

#!/usr/bin/env python3
# compare_local_contrast.py
import os
import argparse
import numpy as np
import matplotlib.pyplot as plt
# Required: tifffile (TIFF読み込みの安定版)
try:
import tifffile as tiff
except ImportError as e:
raise SystemExit("tifffile が必要です。pip install tifffile で入れてください。") from e
# Optional: SciPy (高速な局所平均/分散)
try:
from scipy.ndimage import uniform_filter
HAVE_SCIPY = True
except ImportError:
HAVE_SCIPY = False
# Optional: Pillow (PNG/JPG等の読み込み)
try:
from PIL import Image
HAVE_PIL = True
except ImportError:
HAVE_PIL = False
# Optional: FITS
try:
from astropy.io import fits
HAVE_ASTROPY = True
except ImportError:
HAVE_ASTROPY = False
# Optional: 距離指標(JS divergence)
def js_divergence(p, q, eps=1e-12):
p = np.asarray(p, dtype=np.float64)
q = np.asarray(q, dtype=np.float64)
p = p / (p.sum() + eps)
q = q / (q.sum() + eps)
m = 0.5 * (p + q)
# KL with eps
def kl(a, b):
a = np.clip(a, eps, None)
b = np.clip(b, eps, None)
return np.sum(a * np.log(a / b))
return 0.5 * kl(p, m) + 0.5 * kl(q, m)
def ks_statistic(x, y):
"""Two-sample KS statistic (no p-value)"""
x = np.sort(np.asarray(x))
y = np.sort(np.asarray(y))
n = x.size
m = y.size
# Merge points
allv = np.sort(np.concatenate([x, y]))
cx = np.searchsorted(x, allv, side="right") / n
cy = np.searchsorted(y, allv, side="right") / m
return np.max(np.abs(cx - cy))
def read_image(path):
ext = os.path.splitext(path)[1].lower()
if ext in [".tif", ".tiff"]:
img = tiff.imread(path)
return img
if ext in [".fits", ".fit", ".fts"]:
if not HAVE_ASTROPY:
raise RuntimeError("FITSを読むには astropy が必要です。pip install astropy")
return fits.getdata(path)
if ext in [".png", ".jpg", ".jpeg"]:
if not HAVE_PIL:
raise RuntimeError("PNG/JPGを読むには pillow が必要です。pip install pillow")
return np.array(Image.open(path))
raise RuntimeError(f"未対応の拡張子です: {ext}")
def to_luminance(img):
"""RGBなら輝度へ。単一チャンネルならそのまま。"""
a = np.asarray(img)
if a.ndim == 2:
return a
if a.ndim == 3 and a.shape[2] >= 3:
# sRGBっぽい係数(ざっくり)
r, g, b = a[..., 0], a[..., 1], a[..., 2]
return 0.2126 * r + 0.7152 * g + 0.0722 * b
# それ以外は平均で潰す
return a.mean(axis=-1)
def robust_normalize(x, low_pct=0.1, high_pct=99.9):
x = np.asarray(x, dtype=np.float32)
lo, hi = np.percentile(x, [low_pct, high_pct])
if hi <= lo:
return np.zeros_like(x, dtype=np.float32)
y = np.clip(x, lo, hi)
y = (y - lo) / (hi - lo)
return y.astype(np.float32)
def local_mean_std(img01, window):
"""img01: 0..1 float32"""
if HAVE_SCIPY:
# uniform_filter は O(1) で速い
mu = uniform_filter(img01, size=window, mode="reflect")
mu2 = uniform_filter(img01 * img01, size=window, mode="reflect")
var = np.maximum(mu2 - mu * mu, 0.0)
sigma = np.sqrt(var)
return mu, sigma
# SciPyなし版(遅いけど動く):積分画像で実装
# 端処理は簡易に reflect 近似(pad)
pad = window // 2
x = np.pad(img01, pad, mode="reflect")
# integral image
ii = x.cumsum(0).cumsum(1)
ii2 = (x * x).cumsum(0).cumsum(1)
def box_sum(ii_):
w = window
A = ii_[w:, w:]
B = ii_[:-w, w:]
C = ii_[w:, :-w]
D = ii_[:-w, :-w]
return A - B - C + D
s = box_sum(ii)
s2 = box_sum(ii2)
area = float(window * window)
mu = s / area
var = np.maximum(s2 / area - mu * mu, 0.0)
sigma = np.sqrt(var)
return mu.astype(np.float32), sigma.astype(np.float32)
def compute_local_contrast(img01, window, eps=1e-6):
mu, sigma = local_mean_std(img01, window)
# あなたの定義: local_std / local_mean
lc = sigma / np.maximum(mu, eps)
return lc.astype(np.float32)
def summarize(arr):
arr = np.asarray(arr)
return {
"mean": float(np.mean(arr)),
"median": float(np.median(arr)),
"p90": float(np.percentile(arr, 90)),
"p95": float(np.percentile(arr, 95)),
"p99": float(np.percentile(arr, 99)),
"max": float(np.max(arr)),
}
def savefig(path):
plt.tight_layout()
plt.savefig(path, dpi=160)
plt.close()
def main():
ap = argparse.ArgumentParser()
ap.add_argument("--images", nargs="+", required=True, help="画像パスを並べて指定")
ap.add_argument("--labels", nargs="*", default=None, help="画像ラベル(省略可)")
ap.add_argument("--window", type=int, default=64, help="ローカル統計の窓サイズ(px)")
ap.add_argument("--bins", type=int, default=300, help="ヒストグラムbin数")
ap.add_argument("--crop", type=str, default=None,
help="x0,y0,w,h 例: 1000,2000,3000,2000 (比較を同一領域に固定したい場合)")
ap.add_argument("--ref", type=int, default=0, help="差分の基準画像インデックス(0始まり)")
ap.add_argument("--outdir", type=str, default="contrast_report", help="出力フォルダ")
args = ap.parse_args()
os.makedirs(args.outdir, exist_ok=True)
paths = args.images
labels = args.labels
if labels is None or len(labels) == 0:
labels = [os.path.splitext(os.path.basename(p))[0] for p in paths]
if len(labels) != len(paths):
raise SystemExit("labels の数は images と同じにしてください。")
crop = None
if args.crop:
x0, y0, w, h = map(int, args.crop.split(","))
crop = (x0, y0, w, h)
imgs01 = []
for p in paths:
raw = read_image(p)
lum = to_luminance(raw)
if crop:
x0, y0, w, h = crop
lum = lum[y0:y0+h, x0:x0+w]
img01 = robust_normalize(lum)
imgs01.append(img01)
# local contrast arrays/maps
lcs = []
summaries = []
for img01 in imgs01:
lc = compute_local_contrast(img01, window=args.window)
lcs.append(lc)
summaries.append(summarize(lc.ravel()))
# ===== 1) Overlay histogram (same bins) =====
all_vals = np.concatenate([lc.ravel() for lc in lcs])
# 外れ値で潰れないように上側を少し切る(必要なら調整)
vmax = np.percentile(all_vals, 99.9)
bins = np.linspace(0.0, vmax, args.bins)
plt.figure()
for lc, lab in zip(lcs, labels):
hist, _ = np.histogram(np.clip(lc.ravel(), 0, vmax), bins=bins)
plt.plot((bins[:-1] + bins[1:]) / 2, hist + 1, label=lab) # +1 for log
plt.yscale("log")
plt.title(f"Local contrast distribution (window={args.window}px) overlay")
plt.xlabel("local_std / local_mean (clipped)")
plt.ylabel("Count (log)")
plt.legend()
savefig(os.path.join(args.outdir, "01_hist_overlay.png"))
# ===== 2) ECDF (差が見えやすい) =====
plt.figure()
for lc, lab in zip(lcs, labels):
v = np.clip(lc.ravel(), 0, vmax)
v = np.sort(v)
y = np.linspace(0, 1, v.size, endpoint=False)
plt.plot(v, y, label=lab)
plt.title(f"ECDF of local contrast (window={args.window}px)")
plt.xlabel("local_std / local_mean (clipped)")
plt.ylabel("Cumulative probability")
plt.legend()
savefig(os.path.join(args.outdir, "02_ecdf.png"))
# ===== 3) Summary table (text) =====
txt_path = os.path.join(args.outdir, "03_summary.txt")
with open(txt_path, "w", encoding="utf-8") as f:
f.write(f"window={args.window}px\n")
f.write("label\tmean\tmedian\tp90\tp95\tp99\tmax\n")
for lab, s in zip(labels, summaries):
f.write(f"{lab}\t{s['mean']:.6f}\t{s['median']:.6f}\t{s['p90']:.6f}\t"
f"{s['p95']:.6f}\t{s['p99']:.6f}\t{s['max']:.6f}\n")
# ===== 4) Distance matrices: KS / JS =====
n = len(lcs)
ks = np.zeros((n, n), dtype=np.float64)
js = np.zeros((n, n), dtype=np.float64)
# JSはヒストグラムで近似
hists = []
for lc in lcs:
hist, _ = np.histogram(np.clip(lc.ravel(), 0, vmax), bins=bins)
hists.append(hist.astype(np.float64))
for i in range(n):
for j in range(n):
if i == j:
continue
ks[i, j] = ks_statistic(np.clip(lcs[i].ravel(), 0, vmax),
np.clip(lcs[j].ravel(), 0, vmax))
js[i, j] = js_divergence(hists[i], hists[j])
def plot_matrix(M, title, fname):
plt.figure()
plt.imshow(M, interpolation="nearest")
plt.title(title)
plt.colorbar()
plt.xticks(range(n), labels, rotation=45, ha="right")
plt.yticks(range(n), labels)
savefig(os.path.join(args.outdir, fname))
plot_matrix(ks, "KS distance (local contrast distributions)", "04_ks_matrix.png")
plot_matrix(js, "JS divergence (hist approx)", "05_js_matrix.png")
# ===== 5) Local contrast maps montage (same color scale) =====
# ここも比較が見えるように同一スケールに固定
map_vmax = np.percentile(np.concatenate([lc.ravel() for lc in lcs]), 99.5)
cols = min(3, n)
rows = int(np.ceil(n / cols))
plt.figure(figsize=(5 * cols, 4 * rows))
for idx, (lc, lab) in enumerate(zip(lcs, labels)):
ax = plt.subplot(rows, cols, idx + 1)
im = ax.imshow(np.clip(lc, 0, map_vmax), vmin=0, vmax=map_vmax)
ax.set_title(lab)
ax.set_axis_off()
plt.colorbar(im, ax=plt.gcf().axes, fraction=0.015, pad=0.01)
plt.suptitle("Local contrast maps (same scale)", y=1.02)
savefig(os.path.join(args.outdir, "06_lc_maps_montage.png"))
# ===== 6) Difference maps vs reference =====
ref = args.ref
ref_lc = lcs[ref]
# 差分は見やすいように対称レンジに
diffs = []
for i in range(n):
if i == ref:
diffs.append(None)
else:
diffs.append(lcs[i] - ref_lc)
# 差分の表示スケール
diff_vals = np.concatenate([d.ravel() for d in diffs if d is not None])
dlim = np.percentile(np.abs(diff_vals), 99.5)
m = n - 1
cols = min(3, m) if m > 0 else 1
rows = int(np.ceil(m / cols)) if m > 0 else 1
plt.figure(figsize=(5 * cols, 4 * rows))
k = 1
for i in range(n):
if i == ref:
continue
ax = plt.subplot(rows, cols, k)
k += 1
im = ax.imshow(np.clip(diffs[i], -dlim, dlim), vmin=-dlim, vmax=dlim)
ax.set_title(f"{labels[i]} - {labels[ref]}")
ax.set_axis_off()
if m > 0:
plt.colorbar(im, ax=plt.gcf().axes, fraction=0.015, pad=0.01)
plt.suptitle("Local contrast difference maps (vs reference)", y=1.02)
savefig(os.path.join(args.outdir, "07_lc_diff_vs_ref.png"))
print("Done. Outputs saved to:", args.outdir)
print("Summary:", txt_path)
if __name__ == "__main__":
main()
使用したプログラム見たい場合はこちら”+”をクリック↑
使用方法は、
1 サンプル画像のL画像をTIFF32bitFloatでdataフォルダーに保存
2 以下のコマンドでファイルを指定、window スケール(ex.32)を設定して実行
python compare_local_contrast.py \
--images \
data/NGC1499_Master_PixelMathUI_L.tif \
data/NGC1499_Master_MAS_L.tif \
data/NGC1499_Master_HT_L.tif \
--labels PixelMathUI MAS HT \
--window 32 \
--ref 2
3 同じフォルダーに以下のレポートファイルが生成される
contrast_report/ ├── 01_hist_overlay.png ← 分布重ね描き ├── 02_ecdf.png ← 累積分布(差が分かりやすい) ├── 03_summary.txt ← 数値サマリ(超重要) ├── 04_ks_matrix.png ← KS距離(分布差) ├── 05_js_matrix.png ← JS距離 ├── 06_lc_maps_montage.png ← コントラストマップ並べ └── 07_lc_diff_vs_ref.png ← 基準との差分マップ
5. 結果まとめ
5-1. 星あり画像の結果まとめ
32px
64px
128px
■ window = 32px
| 手法 | コントラスト分布の特徴 | PixelMathUIとの差 |
|---|---|---|
| PixelMathUI | 高コントラスト側が強い | 基準 |
| MAS | HTと非常に近い | 小 |
| HT | MASとほぼ一致 | 小 |
所見
- PixelMathUI は小スケール構造をかなり強調
- MAS は HT に近く、過度な強調は抑制
■ window = 64px
| 手法 | コントラスト傾向 | 安定性 |
|---|---|---|
| PixelMathUI | 高コントラスト側にシフト | やや荒れ |
| MAS | 中庸 | 安定 |
| HT | 中庸 | 安定 |
■ window = 128px
| 手法 | 分布の広がり | 大域構造 |
|---|---|---|
| PixelMathUI | 広い | 強調されやすい |
| MAS | 集中 | 自然 |
| HT | 集中 | 自然 |
星あり画像での結論まとめ
| 観点 | PixelMathUI | MAS | HT |
|---|---|---|---|
| 局所コントラスト量 | 最も高い | 中程度 | 低め |
| 星への影響 | 星周りが強く出やすい | 抑制されやすい | 最も穏やか |
| 微細構造(32px) | 非常に強調される | 自然 | 自然 |
| 中〜大構造(64–128px) | 背景含めて強調 | 構造中心 | 構造中心 |
| 分布特性 | 高コントラスト側に長い裾 | HTに近い分布 | 基準分布 |
| 見た目の印象 | ドラマチック・派手 | 落ち着いて自然 | 控えめ |
| 総合評価 | 表現重視・攻めの処理 | 安定と自然さのバランス | 再現性重視 |
星あり結論(一文)
星を含む画像では、PixelMathUI は局所コントラストを強く作り込み、
MAS と HT は星の影響を抑えた自然な強調に留まる。
5-2. 星なし画像の結果まとめ
32px
64px
128px
■ window = 32px
| 手法 | 差分マップの特徴 | ノイズ傾向 |
|---|---|---|
| PixelMathUI | 全体的に高め | 目立つ |
| MAS | HTとの差がほぼ無い | 低い |
| HT | 基準 | 低い |
重要ポイント
- 星を除去すると MAS と HT は ほぼ同一挙動
- PixelMathUI は星なしでもコントラストを押し上げる
■ window = 64px(星なし)
| 手法 | 差分マップの特徴 | ノイズ傾向 |
|---|---|---|
| PixelMathUI | 構造全体でコントラストが高め | やや目立つ |
| MAS | HTと非常に近いが、構造部のみわずかに強調 | 低い |
| HT | 基準 | 低い |
■ window = 128px
| 手法 | 大域的コントラスト | 印象 |
|---|---|---|
| PixelMathUI | 高い | ドラマチック |
| MAS | 抑制的 | 自然 |
| HT | 抑制的 | 自然 |
星なし画像での結論まとめ
| 観点 | PixelMathUI | MAS | HT |
|---|---|---|---|
| 局所コントラスト量 | 一貫して高い | 中程度 | 中程度 |
| ノイズ傾向 | 背景まで持ち上がりやすい | 低い | 低い |
| 微細構造(32px) | 全体的に高め | HTとほぼ同一 | 基準 |
| 中間構造(64px) | 構造部がやや強調 | HTに非常に近い | 基準 |
| 大域構造(128px) | 背景含めて強調 | 抑制的 | 抑制的 |
| 分布・距離指標 | 明確に異なる | HTとほぼ一致 | MASと一致 |
| 見た目の印象 | 演出的 | 自然 | 自然 |
| 総合評価 | 表現優先 | 構造忠実型 | 構造忠実型 |
星なし結論(一文)
星を除去すると MAS と HT の挙動はほぼ同一となり、
PixelMathUI だけが局所コントラストを積極的に押し上げる。
最終まとめ(比較視点)
| 項目 | 星あり | 星なし |
|---|---|---|
| PixelMathUI | 星と構造を強く演出 | 構造+背景まで強調 |
| MAS | 星を抑えつつ構造を強調 | HTとほぼ同等の自然さ |
| HT | 常に基準 | 常に基準 |
| 差が最も出るスケール | 32px | 32px |
| MASの立ち位置 | HT寄り・安定志向 | HTとほぼ同一 |
最終的なまとめ
今回、PixInsight に新しく追加された MAS(Multiscale Adaptive Stretch) について、
PixelMathUI、STF+HistogramTransformation(HT) と比較しながら、
局所コントラストを中心に定量的な検証を行いました。
その結果、MASは単なる「穏やかなストレッチ」ではなく、
複数の利点を併せ持つ、実用性の高いツールであることが分かってきました。
1. MASの基本的な立ち位置は「HT寄りの安定志向」
局所コントラスト分布を見ると、
MASは 星あり・星なしのどちらにおいても HT に非常に近い挙動を示しました。
- 高コントラスト側が過度に伸びない
- 差分マップでも暴れが少ない
- 星の影響を受けにくい
これらの結果から、MASは
破綻を避ける方向に強くチューニングされたストレッチであることが、
数値的にも裏付けられました。
👉 「HTをより安全に、より賢くしたツール」
という位置付けが最もしっくり来ます。
2. MASは“HDR的な振る舞い”を自然に内包している
MASの大きな特徴として見逃せないのが、
HDR 的なダイナミックレンジ圧縮が自然に行われる点です。
- 明るい領域(星・コア)が過度に潰れない
- 淡い構造が無理なく持ち上がる
- 大域構造と微細構造が同時に成立する
これは今回の検証でも、
- 128px(大域)では穏やか
- 32〜64px(中小スケール)では構造をしっかり拾う
という形で、
スケールごとの役割分担が自然に成立していることから確認できました。
👉 MASは「HDR処理を意識しなくても、結果としてHDR的になる」
そんなストレッチだと言えます。
3. 彩度ブースト効果という“副次的だが大きな利点”
MASを実際に使って感じる特徴の一つに、
彩度が自然に持ち上がるという点があります。
これはMASが、
- 輝度構造をスケールごとに整理したうえで
- コントラストを破綻なく付与する
結果として、
- RGB合成後の色分離が良くなる
- 彩度を強く触らなくても色が乗る
という効果につながっていると考えられます。
PixelMathUIのように
彩度を別途コントロールする必要が少ない点は、
実運用ではかなり大きなメリットです。
👉 MASは
「輝度ストレッチでありながら、色表現にも良い影響を与える」
珍しいタイプのツールです。
4. PixelMathUIは一貫して「表現重視・攻めのストレッチ」
一方、PixelMathUIは今回の検証を通して、
- 全スケールで最も高い局所コントラスト
- 星あり・星なしを問わず、積極的な強調
という特徴が明確でした。
- 微細構造やエッジが立ちやすい
- ドラマチックな表現が可能
- 反面、ノイズやムラも同時に強調されやすい
👉 PixelMathUIは
「意図を持って使うと非常に強力」なツールであり、
MASとは明確に思想が異なります。
5. MASは「迷ったときの最適解」になり得る
今回の検証を総合すると、
- HT:基準・再現性重視
- PixelMathUI:最大限の表現力
- MAS:安定性+HDR性+色乗りの良さ
という関係が見えてきました。
特にMASは、
- 星の有無に左右されにくい
- スケールに対する挙動が一貫している
- 彩度面でも恩恵がある
という点で、
「とりあえずこれを使えば大きく外さない」ストレッチ
と言える存在です。
結論(ひとことで)
MASは、HTの安定性をベースに、
マルチスケール処理・HDR的挙動・自然な彩度ブーストを内包した、
実用性重視のストレッチツールである。
PixelMathUIのように「攻めたいとき」は別として、
自然さ・破綻しにくさ・色の乗りやすさを重視する場面では、
MASは非常に心強い選択肢になると感じました。



















コメント